El cálculo infinitesimal es sin duda la herramienta más potente y eficaz para el estudio de la naturaleza. “El deseo de medir y de cuantificar el cambio, la variación, condujo en el siglo XVII hasta la noción de derivada. El estudio de las operaciones con derivadas, junto con las integrales, constituye el cálculo infinitesimal.” Por otro lado, los orígenes del cálculo integral se remontan al mundo griego; concretamente a los cálculos de áreas y volúmenes que Arquímedes calculó en el siglo III a.C.
LA INTEGRAL
Una de las nociones fundamentales de la integral representa el área bajo la curva. Esta noción surge como una respuesta al cálculo de dicha área
Ésta noción podría generarse de las siguientes formas:
 
Cubriendo el área bajo la curva con círculos, sin embargo existen muchos espacios, que por más círculos que ponga no va a cubrir toda la superficie.
 
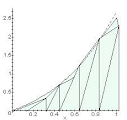
Cubriendo
el área bajo la curva con triángulos, así como con los círculos resulta
complicado, puesto que se tendría que calcular el área de diferentes
triángulos rectángulos o cualquier otro y calcular su área en particular.
Aunque se puede observar que el área que falta por cubrir es menor, sigue
resultando impráctico este método.
Recordando
los diferentes polígonos convexos que conocemos, nos damos cuenta que calcular
el área de un rectángulo es de las más “cómoda”, ¿Qué sucede si realizamos una
aproximación del área bajo la curva con rectángulos?
Por
medio de la siguiente aplicación se puede comprobar, que al hallar el área bajo
la curva por medio de rectángulos, dentro del intervalo [h, g] se aproxima más
a cubrir toda la superficie, Aunque se evidencia unos pequeños espacios, y
debido a ello es necesario hallar el área por exceso, es decir, con rectángulos
que queden por encima de la curva. el valor de ésta área es conocida como suma
superior, y además hallar el área por defecto, que sería con rectángulos que
quedan por debajo de la curva. Luego el valor del área bajo la curva sería el
promedio de ésta dos sumas.
Anteriormente,
como el área de bajo la curva corresponde a una suma de rectángulos, ésta
se representó con el símbolo de la sumatoria
 , el cual luego evolucionó a  .
El
tamaño del error del valor del área dependerá de la cantidad de rectángulos que
dibujemos para hacer la aproximación. A mayor cantidad de rectángulos, las
regiones de cada rectángulo que queden por encima o por debajo serán cada vez
más pequeños que la suma de todos esos errores será despreciable, esto lo puede
comprobar cambiando el valor de n (número de rectángulos) en la aplicación.
|
LA DERIVADA
Una definición del concepto de derivada es que ésta es el resultado de un límite y representa la pendiente de la recta tangente a la gráfica de la función en un punto
El concepto de derivada está íntimamente ligado a el del límite, ya que Para que exista la derivada de una función en un punto, tiene que existir ese límite, cuando no existe ese límite se dice que la función no es derivable en ese punto
Una forma de construir el concepto de derivada es, la de recta tangente a una curva.
Observa el gráfico, en él está representada una función y=f(x) y hemos tomado dos puntos:
La recta BD es una recta secante a la curva cuya pendiente es:
Cuando
la distancia entre B y D se hace más pequeña, es decir, cuando 
tiende a 0, o lo que es lo mismo cuando 
, la recta
secante se convierte en la recta tangente porque corta a la curva en un solo
punto y la pendiente de la recta
tangente será:
tiende a 0, o lo que es lo mismo cuando , la recta
secante se convierte en la recta tangente porque corta a la curva en un solo
punto y la pendiente de la recta
tangente será: 
Ésto lo puedes verificar en la aplicación moviendo C hacia A, y así encontrarás la recta tangente.
Ahora bien, a la pendiente de la recta tangente se le llama derivada de la función en ese punto:
